经典投资组合模型分析及改进
|
于延磊 天津商业大学经济学院 潘旭华 天津商业大学信息工程学院 摘要:在对投资组合的探索过程中,Markowitz首次将投资组合的收益和风险进行了量化,开创了对投资组合研究的新篇章。但由于过于严苛的假设条件,所以其模型在实际生活中并不实用。本文首先对几种经典的投资组合模型进行了综述,然后根据我国的实际情况,引入最小交易单位、交易成本、最大交易量等条件,建立了更符合现实的模型。模型将余额宝纳入投资标的,成功的将投资标的的范围扩展到互联网金融领域。 关键词:投资组合模型;互联网金融;余额宝;交易费用 一、引言 近年来,互联网金融快速发展,特别是2013年支付宝公司推出余额宝以后,人们对投资理财的热情达到了空前的高度。现如今,我国股票市场几经波折又有重新走高的趋势。然而,2008年美国金融危机造成的严重经济衰退在人们心中仍留有阴影。 在投资理财过程中,为了追求高收益、低风险的投资目标,人们往往采取按不同的比例对多种证券进行有机结合的方式,以期获得最大收益的同时将风险控制在一定范围之内。无论是金融机构还是个人投资者都面临着如何在有效控制风险的条件下追求高收益的难题。因此,建立符合我国金融市场的投资组合模型成为现代金融理论的核心问题之一。 二、经典投资组合模型分析 (一)Markowitz均值—方差模型 1、模型简介 Markowitz的均值—方差模型第一次将人们在投资过程中最关心的收益和风险进行了量化处理,成为现代投资组合理论的基础。Markowitz假设证券收益率服从正态分布,并用期望收益率(收益率均值)来衡量未来一段时间证券的实际收益率,以收益率的方差(或标准差)来衡量证券的风险。 Markowitz解决了这样一个问题:如果一名投资者为提高收益降低风险而同时对多种证券进行投资,那么如何确定各证券的投资比例。为解决这一问题,Markowitz认为投资者需要达到这样一个目标:投资者所选投资组合在收益一定时风险最小,或者在风险一定时收益最大,此即为最优的投资组合。 为达到以上目标需做以下几个假设: (1)投资者的目标是效用最大化,即投资者为经济学中的理性人; (2)证券市场中信息是完全流通的,投资者获取信息的成本为零,且每个投资者得到的信息是完全相同的,即证券市场为有效的完全竞争市场; (3)证券的收益率为随机变量并服从正态分布,以收益率的均值和方差来描述其性质; (4)证券之间存在相关性,并以收益率的协方差来描述各证券之间的相关性; (5)没有最小交易单位,即投资者可以购买1/3或1/5股; (6)投资过程中不存在税收和交易费用等成本; (7)投资过程一次性完成,不存在重复投资; (8)存在卖空机制。 设一投资组合中有n种证券,这n种证券的收益率分别为r1、r2、…、rn;期望收益率分别为u1、u2、…、un;每种证券的投资权重分别为w1、w2、…、wn,其中w1+w2+…+wn=1;令En=(1,1,…,1)T,则ET nw=1;向量R=(r1、r2、…、rn)T表示收益率向量值,向量U=E(R)=(u1、u2、…、un)T表示期望收益率向量值;用第i种证券收益率ri的方差σ2 i=D(ri)=E(ri-ui)2表示第i种证券的风险;σij=σji=COV(ri,rj)表示第i种证券和第j种证券的相关系数,V=(σij)n×n为收益率R的协方差矩阵,则投资组合的风险可表示为σ2=D(R)=∑n i=1∑n j=1(wiwjσij)=WTVW(i,j=1,2,…,n)。 在投资组合的预期收益率一定时,风险最小化的模型如下: min σ2= WTVW s.t UTW=u ET nw=1 在投资组合的预期风险一定时,收益率最大化的模型如下: max UTW=u s.t σ2= WTVW ET nw=1 2、模型的不足之处 Markowitz的均值—方差模型为投资组合理论奠定了基础,建立出一套可行的量化方法,进而为投资组合的后续研究指明了方向。然而,Markowitz的均值—方差模型的实用性不强,在证券市场中受到诸多限制。模型局限性主要表现在以下几个方面。 第一,现代投资者对风险的偏好远非模型所描述的多数为风险厌恶型,这是不够全面的;第二,模型的假设条件过于严苛,且多与现实生活不符,例如:以收益率的协方差来描述各种证券间的相关性,以方差来衡量风险,这些都不能被信服;第三,对于大规模投资组合问题,均值—方差模型求解的难度较大,从而导致了计算上的高度复杂性;第四,现实的交易过程中存在交易费用和税收等成本,而均值—方差模型没有考虑交易成本问题,然而忽略交易成本可能会导致无效的投资组合;第五,只有当投资者的效用函数是凹的,或者收益率满足正态分布的条件时,均值—方差模型才与效用理论完全相符合,而这些条件在实际中常常难以满足。 (二)因素模型 Markowitz的均值—方差模型由于由于过于复杂,在实际应用过程中即使采用计算机也常常不能满足实际需求。在均值—方差模型的基础上,Sharpe提出的单指数模型和多因素模型简化了计算过程的复杂性,使投资组合理论的实用性大大增强。 1、单指数模型 单指数模型的基本思想可描述为:证券收益率的变动受一种或几种指数变动的影响,各种证券之间的相互关系由它们与指数的共同关系推出。市场中大多数证券的收益率随指数的走高而升高,随指数的下降而降低。 假设市场作用引起证券价格的变动,可得到如下模型: Ri=αi+βiRm+εi 式中,αi是不受指数影响的收益;Rm是某种指数;βi是证券i的收益率对指数的敏感系数;εi是残差项。 于是,证券组合P的期望收益率为: Rp=αp+βpRm 式中 βp=∑n i=1βixi,αp=∑n i=1αixi,∑n i=1xi=1 其中,xi为投资于证券i的权重。 此时,投资组合P的方差为: σ2 p=β2 pσ 2、多因素模型 在现实生活中,影响证券收益率变动的因素有很多,如通胀、利率的变动、国民生产总值、经济增长等因素都会对证券的收益率产生影响。多因素模型将多种影响证券收益率变动的因素纳入考虑范围,因此,其可以更加准确的描述证券收益率的波动。 多因素模型可表示为: Ri=αi+∑n k=1βi,kIk+εi (i=1,2,…,n) 式中,αi为证券i独立于指数的收益部分;Ik为影响证券收益的第k个指数,并且各指数间是相互独立的;βi,k为证券i的收益率对指数Ik的敏感系数;εi为残差项。 3、模型的局限性 在实际生活中各证券之间的收益率存在相关关系,相互之间也存在一定影响,故投资组合的残差一般不为零,而在单指数模型中却假设投资组合的残差为零。因此,模型的解与现实有一定的差距,精确性较差。 多因素模型从模型的形式上看比均值—方差模型更为简单,比单指数模型更为合理,但仍存在一些问题。首先,多因素模型中各因素敏感系数的求解不确定性较大。其次,因素的收益数据与证券的收益数据存在选取时间区间不同的情况,因此,会增大模型的误差。最后,多因素模型在选取的因素中要求各因素相互独立,而金融市场中各因素之间往往存在相关性,所以模型中各影响因素的选取存在一定困难。 (三)资本资产定价模型 1、模型简介 以Markowitz的均值—方差模型和资本市场理论为基础的资本资产定价模型,主要研究证券市场中证券的预期收益率与风险资产之间的关系,它指出证券的预期收益率就是无风险收益率和风险补偿两者之和,揭示了证券收益率的内部结构。 资本资产定价模型的基本假设: (1)证券市场是一个有效的完全竞争市场,信息是完全对称的,投资者能免费获得所需要的所有信息; (2)投资者以预期效用最大化为目标,即在同一收益率水平下,选择低风险的证券;同一风险水平下,选择高收益的证券; (3)证券的收益率服从正态分布; (4)以证券的均值、方差和协方差来描述证券的性质,每个投资者对证券的性质有相同的认识; (5)具有无风险资产,投资者可以自由的借入无风险资本,并以无风险资本进行风险投资; (6)不存在最小交易单位; (7)不考虑交易费用和税收等交易成本; (8)不存在通货膨胀,且折现率不变; (9)存在卖空机制。 满足以上假设条件的资本资产定价模型为: Rp=Rf+βp(Rm-Rf) 其中Rp是证券组合P的期望收益率;Rm是市场组合的期望收益率;Rf是无风险资产的预期收益率;βp是证券组合的敏感系数(表示资产的回报率对市场变动的敏感程度);βp=θpm/σ 2、模型的局限性 虽然资本资产定价模型在实际的应用中十分广泛,但它也存在明显的局限性。这些局限性产生的原因之一就是其假设条件与实际情况不符,例如:证券市场是完全竞争市场的假设,而实际情况是由于各种交易费用的存在,证券市场为不完全竞争市场;借贷利率相等,且与无风险利率相等的假设,而实际情况是贷款利率大于存款利率等等。另外,模型中的敏感系数代表过去该证券与市场之间的相关性,而投资者关心的是证券未来与市场之间的相关性。我国证券市场发展不够完善,在信息公开化程度、信息披露机制、投资者投资结构和上市公司股权结构等等方面仍不够合理,这些因素都降低了模型的准确性。 (四)套利定价模型 1、模型简介 套利交易是投资者利用同一种资产在不同地域或不同时间内不同价格来赚取无风险利润,最终得到资产的均衡价格,使套利机会消失。而套利定价模型与套利交易无关,它是对资产估值的模型,其核心思想是一项资产的价格受不同因素的影响,各因素对资产价格的影响各不相同,存在不同的敏感系数,用敏感系数与各因素的乘积的加和,再加上无风险利率就可以得到该项资产的价格。 套利定价模型的基本假设: (1) 市场是完全竞争的; (2) 如果存在风险一定而收益可以增加或收益一定而风险可以减小的机会时,投资者就可以利用这一机会建立投资组合; (3) 证券的相关性来源于各种因素的影响,并且证券的收益率与因素之间成线性关系,而且不用明确具体因素是什么; (4) 投资者的预期收益率不一定相同。 在以上假设基础上,套利定价模型可表示为: E(Ri)=λ0+λ1βi1+…+λkβik 其中,E(Ri)表示均衡状态下证券i的预期收益率,λ0、λ1、…、λk为常系数;当市场存在无风险资产时,λ0为无风险收益率Rf;λk为因素fk的风险价格;βik为证券i对因素fk的敏感系数。 2、模型局限性 与资本资产定价模型相比,套利定价模型的假设条件与现实更加接近,但仍存在缺陷。模型中没有给出影响资产价格的具体因素,投资者只能凭借各自经验进行判断选择,此外每种因素都要计算相应的敏感系数,而资本资产定价模型只需计算一个敏感系数。 (五)安全首要模型 二十世纪五六十年代,Roy,Kataoka和Telser在均值—方差模型的基础上提出了三个安全首要模型,在建立安全首要模型时,他们都提出了同一概念——资本极限CL。他们在建立模型时都用到了资本极限CL,CL是最终时刻资本数量Cend的一个下界。 在均值—方差模型的基础上安全首要模型增加了一个投资者愿意接受的亏损极限,在均值—方差模型的基础上投资者对其投资意愿进行选择,使对投资组合的约束更强,进一步缩小了投资范围,使投资者更容易找出满意的投资策略。 第一个安全首要(Safety-First)模型由Roy提出。在Roy所建立的模型中,他先设定出一个资本极限CL,模型在最终时刻的资本量Cend小于或等于资本极限CL的概率最小化。即: min {P(Cend≤CL)} 第二个安全首要(Safety-First)模型由Kataoka 提出。模型中定义了亏损概率——α值。他希望将资本极限CL最大化,使最终资本量Cend低于资本极限CL的概率小于或等于亏损概率。即: max CL s.t P(Cend≤CL)≤α 第三个安全首要模型Telser提出。在第三个安全首要模型中也提出了亏损概率,并取资本的最大值为CL。在给定亏损概率和资本极限的条件下使最终资本量Cend的期望值最大化。即: max E(Cend) s.t P(Cend≤CL)≤α 三、本文模型建立 以上模型的基本假设现实中有的可以满足,有的就得不到满足,从而导致模型失效。如:在我国证券市场中,交易费用和税收等交易成本的存在、非卖空机制和最小交易单位的存在等等都会影响到投资组合模型的精确性。现如今,随着互联网金融的快速发展,互联网金融理财产品成为理财市场的生力军。以下我们将余额宝等互联网金融理财产品纳入我们的投资标的中,建立更为符合我国投资理财环境的投资组合模型。 (一)引入最小交易单位 在我国证券市场的证券交易过程中,股票不是无限可分的,存在最小交易单位,即投资者不可以购买1/3或1/5股,证券的最小交易单位为一手(每手100股),证券的买卖必须是一手的整数倍。因此,在本文中引入最小交易单位xi(i=0,1,2,…,n),xi必须为整数,表示第i种风险证券的投资单位数(股票手数)。在我国证券市场中,禁止买空卖空,故xi大于等于0。以余额宝为代表的互联网金融理财产品没有最小交易单位的限制,在本文中以x0表示余额宝的投资额度。 (二)引入交易成本 上文介绍的几种模型在交易过程中没有涉及交易费用和税收等交易成本。而在现实中交易费用和税收等交易成本的存在足以影响到模型的结果,甚至最终得到无效的投资组合。因此,在投资组合模型中将交易费用和税收考虑在内显得十分必要。下面我们将交易成本引入到模型中。 在我国,交易成本主要包括交易所的各种交易费用、券商的佣金以及印花税。以上海证券交易所A股交易为例,其交易费用主要包括以下三项: (1)经手费:成交金额的0.00696%(双向) (2)证管费:成交金额的0.002%(双向) (3)印花税:成交金额的0.1% (单向) (4)佣金:成交金额的0.35%(单向),成交佣金起点5元,支付给券商 本文以C0(x0)、Ci(xi)表示余额宝和第i种风险证券的交易成本;以k11表示经手费的成本系数,其中k11=0.00696%,,以k12表示证管费的成本系数,其中k12=0.002%,以k1表示经手费和证管费的成本系数的和,即k1= k11+ k12;以k2表示印花税,其中k2=0.1%,卖出时收取;以k3表示佣金,其中k3=0.35%中在卖出时收取;引入 pi作为一单位第i种风险证券的价格,引入xi作为投资者准备购买第i种风险证券的单位数,引入yi作为投资者已持有的风险证券i的单位数。由于余额宝在交易过程中没有交易成本,所以其交易成本函数为零,即: C0(x0)=0 风险证券的交易成本为: Ci(xi)=k1(xi)+k2(xi)+k3(xi) 其中 k1(xi)=2(k11+k12)∣pixi-piyi∣ k2(xi)= k2∣pixi-piyi∣ (三)引入最大交易量 在我国证券市场中,资金注入受到一定的限制,并且由于投资者的资金都有上限,故在投资过程中存在资金的上限。我们引入g表示投资者资金的上限,用x0+∑n i=1 pixi≤g表示对投资组合模型的资金限制,小于等于表示资金可以有所结余。 (四)模型的最终形式 综上所述,本文所建立的投资组合模型如下: max(1-λ)[(r0x0-C0(x0))+∑n i=1(ri pixi-Ci(xi))] -λ[∑n i=1(pixi)2σ2(ri)+∑n i=1∑n j=i+12(pixi)(pjxj)COV(ri,rj)] s.t x0+∑n i=1 pixi≤g x0为非负数 xi为非负整数,(i=1,2,…,n) 其中,σij=σji=COV(ri,rj)表示第i种风险证券和第j风险种证券的相关系数;λ为投资者的风险偏好系数,,λ越小表示投资者只考虑收益而不考虑风险的大小,λ越大表示投资者希望将风险最小化而不考虑收益。余额宝主要以协议存款为投资标的,与各证券的相关性不大,故可假设其与各证券不相关。 四、结语 经典投资组合模型的假设较为理想化,多与现实情况不符,很难较精确地反映我国证券市场实际情况。本文通过对模型假设进行修正,并将交易过程中存在的最小交易单位、交易成本和最大交易量等问题引入模型中并加以解决,建立了一个更为符合我国金融市场的投资组合模型。然而,投资组合模型的优化研究依然存在很多问题亟待解决,如大量的假设多与实际不符、影响证券收益的诸多因素难以定量化处理。此外,如何快速对投资组合优化模型进行求解也是值得我们去研究的一个方向。我们相信随着证券投资理论和智能优化算法等工具的不断发展,投资组合模型一定能得到更好的优化和改进,从而为人们的投资理财发挥更大的作用。 参考文献: [1]Markowitz H.刘军霞,张一弛译.资产选择—投资的有效分散化(第二版)[M].北京:首都经济贸易大学出版社,2000:1-416 [2]Sharpe W .A simplified model for portfolio analysis [J].Management Science,1963(9):277-293 [3]李颖,汤果,陈方正.多因素模型在投资管理中的应用[J].华东经济管理,2002(16)5:95-97 [4]Sharpe W.Capital asset prices:a theory of market equilibrium under condition risk [J].Journal of Finance,1964(19):425-442 [5]Lintner J.The valuation of risk assets and the selection of risky investments in stock portfolios and capital budgets [J].Review of Economics and Statistics,1965,47(2):13-37 [6]Mossin J. Equilibrium in a capital asset market [J].Economica,1966,34(4):768-783 [7]Roll R,Ross S.An Impirical Investigation of the Arbitrage Pricing Theory[J].Journal of Finance,1980,35:1073-1103 [8]Roy A. Safety-first and the holding of assets[J]. Economics,1952,20 (3):431-449 [9]Pyle D,Turnovsky S. Safety-first and expected utility maximization in mean standard deviation portfolio analysis[J].The Review of Economics and Statistics,1970,52(1):75-81 [10]Telser L.Safety first and hedging[J].Review of Economic Studies,1956,23:1-16 [11]上海证券交易所官方网站[EB/OL] |






 浅析我国非营利组
浅析我国非营利组 财务公司模式在高
财务公司模式在高 中国对外直接投资
中国对外直接投资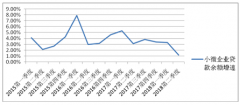 关于中小企业融资
关于中小企业融资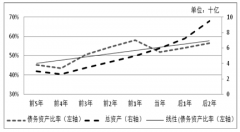 债权融资对北京市
债权融资对北京市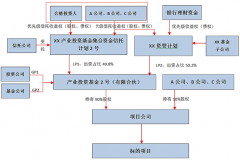 PPP基金模式中“
PPP基金模式中“