基于电商平台爬虫数据的面粉价格指数预测
|
雷兵 王静华 (河南工业大学管理学院,河南 郑州 450001) 摘要:随着网络零售的发展,电商平台面粉的交易数据越来越庞大,为了监测电商平台面粉价格走势,使用爬虫技术采集面粉大数据,并根据合适的价格指数计算公式计算出各期价格指数,再利用时间序列预测模型对其预测十分必要。本文通过网络爬虫技术采集京东平台的面粉数据,再改进加权价格指数计算方法以获得各期电商评分价格指数,最后再构建时间序列模型ARIMA和ARIMAX预测面粉价格指数走势。 关键词:爬虫数据;电商面粉;价格指数;预测分析 价格指数是反映物品价格变动的晴雨表和风向标,是窥探行业发展情况的有效指标。2024年中央一号文件及“十四五”规划中均明确提出,要确保粮油市场稳步发展,保障粮油价格平稳波动。同时,伴随着互联网技术的普及和发展,网络零售市场以电子商务为媒介而迅速壮大,不少粮油企业选择在电商平台开设店铺来销售粮油商品。面粉作为粮油食品的重要组成部分,在粮油食品中占据很大比例,对提供居民营养所需、保障生活质量有着不可或缺的作用。因此,通过电商平台获取面粉销售信息大数据,再对其价格走势进行分析十分重要。 电商平台面粉价格指数有别于传统价格指数,表现在数据来源新,电商面粉价格指数使用网络零售大数据来获取面粉数据,将数据来源从传统的线下走访或调查转移到线上采集,拓展了数据获取渠道。另外,在获取到电商面粉大数据后,本文针对其特性对价格指数计算方法进行了一定的改进,使其更好的反映网络电商平台面粉的价格变动情况,最后本文使用经典的差分自回归移动平均模型(ARIMA)和引入外生变量的差分自回归移动平均模型(ARIMAX)来预测电商平台面粉价格走势,可为电商平台粮油商家和网购消费者提供可行建议。 一、文献回顾 在价格指数预测之前,需要选择价格指数计算方式来明确基期和报告期价格指数具体值,之后再构建合适的预测模型来预测价格走势。目前,对指数计算的研究主要集中在拉氏价格指数和帕氏价格指数。如刘宇娟在计算基于大数据的公路货运价格指数时,分别使用拉式价格指数和帕氏价格指数两种方法计算出三级公路货运价格指数,完善了货运动态价格指数的研究。褚晓琳在研究我国商品期货的价格指数时,从商品期货的品种选择、指数权重设计及调整等方面对比分析了拉式价格指数和帕氏价格指数在编制期货价格指数是的优缺点,认为两者在计算期货价格指数时均有一定意义。上述加权价格指数计算所牵涉的主体集中在传统商品上,较少应用到网络零售商品的价格指数计算,另外,加权价格指数计算时还要求被调查商品在基期和报告期内连续出现,保证计算公式的成立。但是,电商数据通常不具备上述条件,不能满足上述要求,基于此,部分学者对加权价格指数计算方式进行了改进。朋琳在计算大家电价格指数和有色金属价格指数时,为了保证基期和报告期被调查数据的连续型,将两期商品数据进行汇总求交集,以得到在基期和报告期内均存在连续价格和销量值的数据,这种方法显然满足了加权价格指数计算要求,但应用在电商面粉大数据时,每期数据采集量能达到万条以上,如果预测价格指数的长期变动情况,那么在合并数据时会浪费巨大的算力。 通过梳理价格指数计算方式相关文献后,本文对加权价格指数计算方式进行了改进,使其更好的应用在电商平台面粉价格指数计算中。本文的研究目的是为了预测电商面粉价格走势,因而需要构建较好的时间序列预测模型来对价格指数预测,典型的时间序列模型为差分自回归移动平均模型ARIMA,如何文琪在预测我国煤炭价格时,构建了ARIMA(3,1,0)预测模型对煤炭周度价格值进行了预测分析,经实证研究,得到的预测结果精度较高。原云霄等人通过构建ARIMA(1,1,1)对我国服务价格指数的月度数据进行预测,经服务价格真实数据验证,该预测模型的预测误差保持在合理范围内,可以作为服务价格指数预测的分析工具。此外,在构建时间序列预测模型时,不少学者在ARIMA模型的基础上,通过引入外生变量X来构建多元差分自回归移动平均模型(ARIMAX)以获得更精确的预测效果。喻谦花等人在预测城市内涝积水深度时,引入了降雨量这一外生变量构建ARIMAX模型,通过实验数据验证得到该模型的预测精度要高于ARIMA模型,在预测城市内涝积水深度时效果更好。王向前等人在预测港口货物吞吐量时,先使用皮尔逊相关系数筛选出与货物吞吐量关联性最大的六个变量,在此基础上构建了ARIMAX预测模型,经验证,该模型要比不加入相关变量的ARIMA预测模型精度更高、预测误差更小。另外,在梳理上述文献时,注意到确定预测模型的超参数时,通常使用观察时间序列自相关图和偏自相关图来确定移动平均项和自回归项,这种方法过于主观,并且存在部分参数组不能通过参数检验的情况。为解决这一问题,相关学者通过使用网格搜索方法来优化参数确定过程,如闫政旭在预测股票价格时,通过网格搜索确定决策树参数,极大缩短了建模时间,提高了效率。王占平在预测集装箱海运价格时,使用网格搜索方法确定数据挖掘算法中的关键参数,提升了数据挖掘建模效率。 在综合分析上述文献后,本文在分析爬虫数据特性的基础上,综合拉氏价格指数和帕氏价格指数的优点,改进了指数计算方法以使其符合电商平台面粉价格指数计算,另外,在预测电商面粉价格指数时,分别构建ARIMA和引入外生变量的ARIMAX时间序列预测模型,再根据评估指标来对比分析两种预测模型的预测误差,以此确定更适合电商平台面粉价格指数变动的预测模型。 二、爬虫数据来源及预处理 1.数据来源 在预测电商平台面粉价格走势之前,需要获取各期的面粉网络零售数据。当前国内电商平台主要包括京东、天猫、苏宁和拼多多,考虑到京东平台的面粉商品覆盖面较广,且面粉商品描述信息比较完善,故而使用网络爬虫采集京东平台的面粉数据,数据项包括面粉销售价格、面粉优惠价格、面粉规格、面粉销量、面粉评价数等。本文在采集数据时,使用八爪鱼爬虫工具爬取了京东平台面粉类目下的所有面粉商品零售信息,采集时间线为2022年9月17日到2023年2月4日,每隔一周采集一次面粉数据,共采集到23期面粉数据,采集总量为357884条,每期的采集量都保持在10000条以上,平均每期的采集量为15560条。 2.数据预处理 在采集23期电商平台面粉数据后,需要对数据进行预处理以便后续价格指数计算和预测。预处理的主要步骤包括处理重复值、空值和异常值三部分。在处理重复值方面,京东平台会为每个面粉商品提供唯一的库存单位标识(SKU ID),因此可根据面粉商品SKU ID的唯一性来检验面粉的重复情况,经检验发现2022年9月17号这期的数据中第6条、第9条、第162条和第4721条面粉的SKU ID均为“635495252311”,此时将第一条面粉数据保留,并删除后三条重复数据。在处理空值时,需要检验的特征项为商品价格、商品规格和商品销量,商品价格(如20元、25元)是构建和预测价格指数的核心,当缺少价格值时要删除该条数据。商品规格(如1kg、1.5斤、800g)是计算商品单位价格的关键依据,当缺少规格值时也要删除该条数据。商品销量(如20、50袋)是确定价格指数权重的主要依据,当缺少销量时需检查对应的商品评价数是否缺失,若存在则将其试作商品销量,否则删除该条数据,综合来讲,当面粉数据的上述三项特征值有一项为空,则删除该条数据。最后,先直接删除不符合现实情况的商品数据,比如某个面粉商品的销售单价为-1元/KG的情况,再将面粉单价高于100元/KG的数据剔除。之后,再基于3σ原则检验和剔除异常值,具体步骤为先求出本期面粉价格的均值和标准差,并以均值加减3个标准差作为异常值的边界,将大于均值加3个标准差以及小于均值减3个标准差的面粉数据视为异常值,在检验时将其剔除。 三、基于电商平台爬虫数据的面粉价格指数预测及分析 1.选择价格指数计算公式 目前应用最广泛的加权价格指数有两种,分别是拉氏价格指数和帕氏价格指数。本文考虑到电商平台面粉的销售情况容易受到电商活动、舆论热点等影响,其各个时间段内的销量变动幅度相对较大,那么在设计价格指数计算方法时就需要注意报告期内面粉销量较大导致的指数异常的情况。另外,现有的加权价格指数计算公式有一个计算前提,即每期的商品数量一定,且商品要具备可追溯性,然而,通过网络爬虫获取的电商商品数据会由于商家库存管理、平台反爬机制更新等出现各期商品价格不连续、各期商品数量不相等的情况。面对以上现实情况,本文对拉氏价格指数和帕氏价格指数进行了改进,以确保其适合电商面粉的价格指数计算,且能够真实的反映电商平台的价格变动情况,具体如式(1)所示: 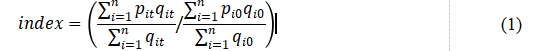 其中,pit、qit表示第i种商品报告期的价格和销量,pi0、qio表示第i种商品基期的价格和销量。 本文改进的加权价格指数计算方式具备两方面的优点:第一,综合了拉氏价格指数和帕氏价格指数,消除了爬虫数据导致的各期商品数量不一致、商品价格不连续的影响,可以更合理地反映不同时间段内电商平台面粉商品价格的平均情况。第二,有力解决了面粉商品销量过大导致的商品价格指数偏高的极端问题,使得各期的价格指数更均衡,更有代表性。 2.计算价格指数 首先,将采集到的第一期京东平台面粉数据确定为基期,后续二十二期面粉数据为报告期,从而确定报告期相对于基期的面粉价格相对变动情况。其次,获取并计算价格指数的关键数据项,包括单位价格和销量,在获取单位价格时,使用面粉的销售价格减优惠价格已得到实际销售价格,之后在使用计算得到的面粉实际销售价格除以面粉规格来获得面粉单位价格,在获取销量情况时,先检查是否存在单位换算,若存在则使用正则表达式提取数据中的整型数据,然后将其换算成对应的销量值,若不存在单位换算时,需要再提取整形数据后删除非中文字符以得到最终销量值,如将“1万+”转化成“10000”,将“5000+”转化为“5000”等,当面粉商品的销量不存在时可以使用面粉评价数近似替代。最后,使用式(1)计算出各期面粉商品单价与销量的乘积之和,然后再除以销量和来得到本期电商面粉的价格总趋势,再将报告期的价格总趋势和机器价格总趋势做除法以得到各期的价格指数值。 3.构建面粉价格指数预测模型 本文以计算得到的各期电商面粉价格指数为实验数据,随后构建了ARIMA模型和引入外生变量的ARIMAX模型,并对两模型的预测误差进行记录,以此来对比分析所构建模型的预测精准度。 (1)基于ARIMA模型的面粉价格指数预测 首先,检验指数平稳性并确定差分情况:本文使用python中statsmodels.tsa.stattools的adfuller()函数对面粉价格指数进行检验,得到的结果为:ADF单位根检验面粉价格指数的t统计量p值为0.511,大于显著性检验水平0.05,表明面粉价格指数的原始数据未通过检验。之后对其进行一阶差分,此时的t统计量p值为0.177,依旧大于显著性检验水平0.05,意味着一阶差分后的面粉价格指数也未通过ADF检验。最后使用ADF检验二阶差分的面粉价格指数时,t统计量p值为0.0026,远小于显著性检验水平0.05,表明此次检验通过了5%水平下的显著性检验,面粉价格指数具有平稳性,由此可将ARIMA模型中的差分项d设置为2。 其次,需要进一步确定自回归项p和移动平均项q:为了节省建模时间,提高模型构建销量,同时考虑到使用价格指数自相关图和偏自相关图这种主观判断带来的误差,本文通过网格搜索方法来确定时间序列模型的参数值。具体步骤为先创建参数网格,一般来说,p和q的取值不超过价格指数数据集长度的十分之一,本文的数据集为20,则p和q的取值不应当超过20/10=2,即p和q的取值范围在0,1,2之间,同时根据ADF单位根检验可以确定差分项d=2。然后确定评估标准来确定最优参数组合,本文使用平均相对误差(RME)来评估,RME计算公式如式(2)所示,网格搜索结果如表1所示,其中参数组(0,2,0)、(1,2,1)、(1,2,2)、(2,2,0)和(2,2,2)的平均相对误差值均大于0.15,表现结果不优良,将这几组参数组合舍弃,选择剩下的几组进入后续筛选。  其中,n是面粉价格指数测试集个数,Yi是面粉价格指数实际值,Yi是面粉价格指数的预测值。 表1 网格搜索结果  最后,确定最优参数组合并预测价格指数。将筛选后的参数组合带入ARIMA模型进行回归检验,结果显示,只有参数组(1,2,0)的各个回归参数通过了显著性检验,该参数组合为最优的ARIMA参数组合,即构建模型的自回归项、差分项和移动平均项分别为1、2和0,然后再对构建的模型进行白噪声检验以确保模型能有效提取信息,本文使用ljung-box方法检验模型残差是否为白噪声,最终检验结果表明LB统计量在一阶滞后和二阶滞后的p值分别是0.1604和0.2761,均大于显著性水平0.05,则拒绝残差为非白噪声的假设,表明构建的模型有效提取到指数序列信息。最后将电商面粉价格指数数据集划分为训练集和测试集,其中第1-20期为训练集,最后3期为测试集,使用ARIMA(1,2,0)并通过静态预测的方式预测出后3期价格指数值,并将预测值和真实值按照平均绝对误差(MAE)、均方误差(MSE)和平均绝对百分比误差(MAPE)的评估标准计算出预测误差,MAE、MSE和MAPE的计算公式如式(5): 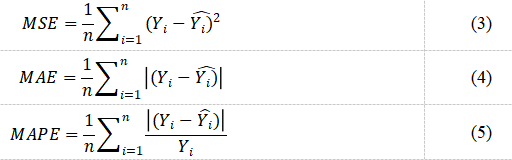 其中,n是面粉价格指数测试集个数,Yi是面粉价格指数实际值,Yi是面粉价格指数的预测值。 ARIMA(1,2,0)模型的预测具体情况为:第21期、22期、23期的真实值分别为8.6691、8.8991和8.8877,预测值分别为9.1234、8.7128和8.7726,预测误差方面,第21期的平均绝对误差为0.4548、均方误差为0.2069、平均绝对百分比误差为0.0525,第22期的平均绝对误差为0.1862、均方误差为0.0347、平均绝对百分比误差为0.0209,第23期的平均绝对误差为0.1169、均方误差为0.0137、平均绝对百分比误差为0.0131,综合来说,使用ARIMA(1,2,0)的平均绝对误差为0.2527、均方误差为0.0851、平均绝对百分比误差为0.0288。 (2)基于ARIMAX模型的面粉价格指数预测 首先,引入外生变量并检验协整性。为了增强预测模型的解释性,提高预测的精准度,本文引入的外生变量为面粉原料价格指数,共采集了23期面粉原料价格指数,并将采集的日期确定为采集电商面粉的前两周,以保证面粉原料价格变动影响电商平台面粉的价格变化。随后,对面粉原料价格指数和面粉价格指数进行协整检验,具体步骤为先建立电商平台面粉价格指数与原料价格指数的回归模型,再对回归后的残差进行单位根检验,以探究变量之间是否存在协整关系。经检验,两变量回归之后残差的t统计量为-3.001,p值为0.035,小于显著性检验标准0.05,表明两变量之间存在协整关系,可以构建ARIMAX时间序列预测模型。 其次,确定模型参数。使用前节提到的网格搜索方法,遍历27组参数的建模表现情况,根据RME输出结果,此次网格搜索过程中共有8组参数的表现较好,分别是(0,2,2)、(1,2,1)、(2,1,0)、(2,1,1)、(2,1,2)、(2,2,0)、(2,2,1)、(2,2,2),随后将八组参数带入时间序列模型以检验各项参数是否通过显著性检验,对于通过检验的进行保留,否则判定改组参数不是最优参数模型,经带入检验,参数组合(2,1,0)的各项参数均通过5%水平下的显著性检验,则ARIMAX模型的自回归项、差分项和移动平均项分别为2、1和0,然后再对该参数组合的残差白噪声进行检验,检验结果中,LB统计量为2.718,对应p值为0.2895,大于显著性水平0.05,则拒绝模型残差是非白噪声的假设,即构建的ARIMAX(1,2,0)模型可以有效提取变量信息。 最后是使用构建的模型进行预测,具体情况为:第21期、22期、23期的真实值分别为8.6691、8.8991和8.8877,预测值分别为8.6525、8.9491和8.9496,预测误差方面,第21期的平均绝对误差为0.2352、均方误差为0.0553、平均绝对百分比误差为0.0265,第22期的平均绝对误差为0.0614、均方误差为0.0038、平均绝对百分比误差为0.00069,第23期的平均绝对误差为0.0679、均方误差为0.0039、平均绝对百分比误差为0.0070,综合来说,使用ARIMA(1,2,0)的平均绝对误差为0.1195、均方误差为0.021、平均绝对百分比误差为0.0134。 (3)对比分析 分别使用时间序列ARIMA和ARIMAX模型对电商面粉价格指数进行预测,其中,ARIMAX模型的预测误差MAE、MSE、MAPE分别是0.1195、0.0851和0.0288,低于ARIMA模型的0.2527、0.0851和0.0288,表明引入面粉原料价格指数的预测模型要优于传统的ARIMA模型。 四、结论 通过预测电商平台面粉价格指数的变动情况,可以为电商商家和消费者带来一定参考。对于电商商家来说,电商平台面粉价格指数的研究能帮助掌握平台面粉的价格走势,从而制定更加精准的面粉商品运营策略,以此增加营收,对于网购消费者而言,消费者可以通过面粉价格指数了解到平台面粉的价格变动情况,适当调整选购计划,合理安排物资的购买。 参考文献: [1]刘宇娟.基于大数据的公路货运实时价格指数研究[J].经济研究导刊,2020(10):141-144. [2]褚晓琳,王家晨,郭志强.我国商品期货价格指数编制方法的现状与国际比较研究[J].中国证券期货,2021(4):86-96. [3]朋琳.大数据在价格调查中的应用研究[J].调研世界,2017(4):3-10. [4]原云霄,王宝海.基于ARIMA模型对我国服务价格指数的预测[J].数学的实践与认识,2018(7):130-137. [5]喻谦花,冯峰,罗福生等.基于ARIMAX的开封“7·20”特大暴雨城市内涝预报研究[J].人民黄河,2022(10): 40-45+50 [6]王向前,吴东隆,郑健彤等.货物吞吐量预测的改进ARIMAX方法——以天津港为例[J].运筹与管理,2022(3):138-144. [7]何文琪.基于ARIMA和线性回归组合模型的煤炭价格预测[J].中国管理信息化,2021(1):187-188. [8]王战平,冯扬文,朱宸良等.基于数据挖掘技术的信息分析方法研究——以集装箱海运价格预测为例[J].情报科学,2019(7):65-71. |






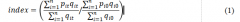 基于电商平台爬虫
基于电商平台爬虫 顾客不文明行为的
顾客不文明行为的 数字普惠金融对中
数字普惠金融对中 企业绩效考核与薪
企业绩效考核与薪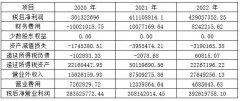 基于EVA的三只松
基于EVA的三只松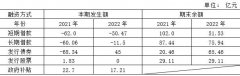 企业投融资决策中
企业投融资决策中