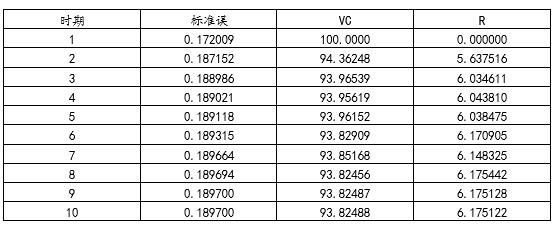
龙健雄  广州大学

摘要：本文以收益率和成交量变动幅度为指标，使用2010-2022年的数据，对创业板指数价与量之间的关系进行研究。基于这两个指标创建VAR（5）模型并进行格兰杰因果检验，然后依据脉冲响应图与方差分解表进一步探究二者关系。得如下结论，成交量变动幅度的滞后期不能影响当期收益率，反之不成立；当自身或对方受到一个冲击时，两者都在初期迅速做出反应，响应持续5-9个交易日后消失，并且两者的方差分解结果显示自身贡献率均超过90%。

关键词：创业板指数；成交量变动幅度；收益率；格兰杰因果检验；向量自回归模型

一、创业板指数出现的背景

20世纪末21世纪初，随着网络的迅速发展，许多国家和地区兴起了以新一代信息技术为主的创业热潮，而美国的纳斯达克市场的顺利运行，给亚洲四小龙中的香港、韩国等发达国家（地区）的证券机构提供了很好的模板，他们纷纷开设了接纳科技创业型企业的创业板。2001年后，美国网络泡沫破灭，以上几个国家或地区的创业板受到重创，紧接着，中国实行股权分置改革，与此同时遭受十分严重的国际金融危机，直至2009年10月下旬，创业板被深圳证券交易所正式挂牌。

截止2010年5月底，一共有88家公司在创业板发行。由于拥有足量样本，在2010年6月初，创业板指数被深圳证券交易所发布，其中，作为主指数的价格指数（即“创业板指”），代码为“399006”。

二、量价关系的相关研究

在中国，投资者参与我国股票市场的较好的股票分析手段是技术分析。其原因有以下两点：一是经验与技巧在该方法中占有重要的地位；二是该方法能灵活适应任何市场。技术分析中有4个要素，分别是：量、价、时、空。量价分析则是其中的两种要素“量”与“价”的配合。 “量在价先”、“量价配合”体现出了量价关系研究的重要性。

根据对于现有的关于股票市场的文献的总结，对于股价的处理是，通过计算，把股价变为收益率，或者是收益率的绝对值。因此，可以发现，探索量价关系，主要从下面的3个方向入手：

（1）研究成交量和股票价格或收益率的相关关系；

（2）研究成交量与股价或收益率的波动性的关系；

（3）研究成交量变动幅度与收益率的关系。

最早研究量价关系的是Osborne（1959），他率先从统计学的角度来建立模型，并且采用物理方法，使股票价格的变动过程通过扩散现象来体现，发现股票价格变化绝对值与股票交易量变化存在正的相关关系。Clark（1973）建立了MDH模型，该模型的核心思想是：股票交易量的波动和股价波动由一个相同的且不可直接观测的市场信息所导致，市场信息的出现将会对股价和交易量同时产生冲击，从而引起这两者的波动。

另外，也有很多学者将股价转化为收益率来研究量价关系。成交量和收益绝对值的同期正相关的关系被Crouch（1970）证实同时出现在个股和指数。Karpoff（1987）使用股票收益率变化量的绝对值和成交量作为价量分析的指标，发现两者有明显的正相关。Shiu-Sheng Chen（2012）使用S&P 500 Index的月度数据，认为牛、熊市的成交量均能被收益率所预测。

近年来，国内学者也研究起了量价关系。熊连庆、刘煜辉（2004）使用中国市场指数，在成交量和成交量的滞后项中同时发现有关收益率方差方面的信息。郑方镳（2007）等采用沪深股市225只股票作为样本，成交量高的交易日的收益率在之后交易日中“反转”的现象同时存在平衡市、熊市、牛市中。

格兰杰因果检验也是学者用来研究收益率与成交量的关系的重要方法。张维、闫冀楠（1998）的研究结果表明，在沪市中收益和交易量之间存在单向的线性因果关系，即此关系仅存在于收益对交易量。邓怡、周紫焱（2015）使用VAR模型，对上海A股市场量价关系进行研究发现，成交量和股价在长期中关系不明显，但在短期内，股价对成交量有剧烈的影响，反之则较为微弱，另外，二者具有双向格兰杰因果关系。南梦佳、王璐熠（2016）使用上证综指和深证指数成交量和收盘价进行方差分解研究，发现二者对对方的贡献率差别很大，成交量对于收益率的贡献率仅为1%，相反则高达20%。史晓雁（2019）对上证指数、深证成指、中小板指数的成交量和收益率进行因果关系研究发现，量与价的关系不存在对称性，收益率的变动引起的成交量的变动程度高于成交量的变动引起收益率的变动程度。

综上所述，股票的价与量之间确实存在某种具体的关联，但是大多数文献研究的量价关系都是基于A股、B股市场或是深证综合指数和上证综合指数来研究，涉及到创业板指数的相对来说比较少。

本文借助向量自回归模型，通过格兰杰检验、脉冲响应以及方差分解分析等统计手段来分析创业板指数成交量和收益率之间的关系并提出有关的投资建议。

三、数据处理

本文的数据来源于锐思数据库（网址：http://www.resset.cn/），选取了我国创业板指数的每日收盘价及其成交量进行实证分析，样本期间为自创业板指数发布日2010年6月1日至2022年9月2日。各变量定义具体如表 1所示。

表1 定义变量表

（一）收盘价

使用Eviews10软件画出创业板指数每日收盘价（P）的走势图，如图 1所示。从图中可以看出，收盘价具有较大的波动性，不适合直接使用收盘价来建立模型。

图1 每日收盘价时间序列图

（二）收益率

道氏理论表明，收盘价可被用于计算收益率。一般情况下，计算收益率的方式有以下2种，一为简单收益率，二为对数收益率。本文采取的是对数收益率的方法，原因主要有以下三点：

（1）具备对称性、收益累加性两大特性。

（2）对数据取对数能够增加数据的平稳性，以及消除异方差对实证结果的影响。

（3）受极端值的影响较收盘价更小，误差更小。

本文使用公式（2.1）计算对数收益率：

其中，Rt表示第t期的对数收益率，Pt表示第t期的收盘价。

图2 对数收益率时间序列图

图3 对数收益率直方图

1.“集群”现象

“集群”现象是指在某一段区间内波动幅度比较大而在另外一些区间内的波动幅度比较小，即波动性表现出了聚集的现象。如图 2所示，创业板指数的对数收益率表现出了“集群”的现象，在第2981个样本左右（即2015年6月到8月）的区间内表现出了较其余区间大的波动聚集性。

2.“尖峰厚尾”现象

由表 2可知：第一，对数收益率（R）的均值为0.000513，比0大，但接近于零。第二，偏度系数为-0.371298，小于0，呈现出负偏态，这在图 3中也不难看出，右侧的尾部明显比左侧的尾部要短。而峰度系数为4.752304，明显比3大，相对于正态分布，呈现出尖峰的形态。综上所述，创业板指数的对数收益率的分布具有“尖峰厚尾”的特点。第三，由J-B统计量可知，由样本推断的总体分布，并没有服从正态分布。

表2 对数收益率统计指标

（三）成交量

由图4可以看出，原成交量序列存在着时间趋势。

图4 成交量时间序列图

为了去掉时间趋势的影响，并且消除异方差对实证结果的影响，本文采取张维、闫冀楠（1998）对于成交量序列的处理方法，定义成交量变动幅度VC为：

其中，VCt表示t期的成交量变动幅度，in Qt是指t期的对数成交量。

图5 成交量变动幅度直方图

由表3可知：第一，成交量变动幅度（VC）的均值为0.000692，比0大，但非常接近零。第二，偏度系数为0.329823，大于0，呈现正偏态，这在图 5中也不难看出，右侧的尾部明显比左侧的尾部要长。而峰度系数为5.427222，明显比3大，相对于正态分布，呈现出尖峰的形态。综上所述，创业板指数的成交量变动幅度的分布具有“尖峰厚尾”的特点。第三，由J-B统计量可知，由样本推断的总体分布并不服从正态分布。

经过上述的数据处理，本文对于创业板指数的量价关系的分析，取对数收益率和成交量变动幅度作为研究对象。

表3 成交量变动幅度统计指标

四、实证研究

首先运用ADF检验的方法，对时间序列进行了平稳性检验，确保所用的时间序列数据是平稳的，避免发生伪回归现象，进而采用VAR模型、脉冲响应函数、方差分解分析等方法来研究收益率与成交量变动幅度之间的关系。

（一）平稳性检验

本文采取Dickey（1979）提出的ADF检验（Augment Dickey-Fuller test），该检验适用于至少阶数为一阶的自回归过程。ADF检验模型如下：

对收益率序列和成交量变动幅度进行ADF检验结果如表4：

表4  收益率、成交量变动幅度ADF检验结果

经过检验发现，R和VC两个序列均同时在1%、5%、10%的显著水平下接受不存在单位根的备择假设，即R与VC这两个时间序列均为平稳时间序列，可被用来建立向量自回归模型。

（二）向量自回归模型

VAR模型是Sims（1980）在20世纪80年代初提出的，其假定是：在该模型中，所有的变量均为内生变量。其一般形式为

Y为内生变量向量，μ为常数项列向量，ε为随机误差列向量，A为参数矩阵。

对于VAR模型来说，滞后期的选择相当重要。首先，为了使所用来构造模型的变量的信息能够被充分地利用，我们应该选择足够多的滞后期。其次，若所选的滞后期数太大，则在整个向量自回归模型里，需要估计更多的参数，进而使模型自由度变少，再加上所掌握的数据有限，就会导致模型的估计不够准确。通常我们使用以下三种方法来确定VAR模型的滞后阶：

（1）根据信息准则越小越好（即AIC、SC的值越小越好）。

（2）根据LR统计量来确定。

（3）以随机干扰项最终为白噪声过程为准则来确定。

表5  VAR模型滞后阶数的选择

根据表 5可知，使用的信息准则不一样，所需要滞后的阶数（表中带有*的）也不一样。依据SC准则，滞后5阶最为合适。依据HQ准则，滞后7阶更为恰当。依据FPE、AIC准则或LR检验，则需要滞后15阶。

如果选择滞后15阶，则需要估计的参数有

K+PK2=2+15x4=62个    （9）

其中，K为模型中所包含的变量个数，P为自回归的滞后阶数的最大值。

由式（9），若建立VAR（15）模型，将会因待估参数过多而损失相对较多的样本容量。另外，根据Lutkepohl（2005）的研究发现，若依据FPE和AIC，则可能会过高估计模型的滞后阶数，而SC准则与HQ准则均可提供对模型的真实的滞后期数的一致估计。所以，本文选择根据SC准则，确定构建VAR（5）模型。

（三）向量自回归模型稳定性检验

在建立VAR模型之后，为了确保脉冲响应函数有效，需要对模型的稳定性进行检验。本文选择的是AR根估计的方法。其判断方法是：当所有的点都落入半径为1的圆里，则可以断定该模型稳定；反之，则不稳定。由图 6可以知道，所有的点均落入单位圆中，表明所估计的VAR（5）能够满足稳定性条件，其输出的收益率与成交量变动幅度之间的关系在统计上具有非常有力的支持。

图6 VAR模型稳定性检验

（四）格兰杰因果关系检验

为了研究创业板指数的成交量变动幅度和收益率这两个变量在时间上的相互影响关系，本论文采用了格兰杰检验的统计方法。若成交量变动幅度的滞后期能够对收益率的当期产生影响，则可以说明前者是后者的格兰杰原因；反之一样。

表6 格兰杰因果检验结果

根据表 6，由P值可知，在显著性水平为1%的情况下，接受“VC不是R的格兰杰原因”的原假设，拒绝了“R不是VC的格兰杰原因”的原假设，即创业板指数成交量变动幅度的滞后期不能影响其当前的收益率，但创业板指数收益率的滞后期可以影响其当前的成交量变动幅度，两者之间存在着单向因果关系，得到与“量在价先”相反的结论。

（五）脉冲响应分析

为了考察所构建的VAR（5）里的成交量变动幅度和收益率这两个变量的随机误差项受到冲击后，对自身以及另一个变量的当前值和未来值的影响，本文使用脉冲响应分析的方法。另外，使用该方法，可以反映出这两个变量的影响方向及程度。由于不同的变量顺序，会影响到脉冲反应函数的估计，为了避免出现这种情况，本论文采用的是广义冲击反应函数（Generalized Impulse Responses）来估计成交量变动幅度和收益率间的动态关系。

本文共追溯10期，横轴是滞后期数，纵轴是变量在受到一个标准差大小的冲击后的反应程度，实线是脉冲响应函数曲线，虚线是加减2倍标准差的置信区间。

图7 收益率对自身的脉冲响应图

如图7，当收益率受到一个正向冲击，收益率自身在初期表现出非常强烈的正向效应，并且达到了正响应的最大值，第2个交易日正向效应迅速减弱，直至第3个交易日时正向效应消失，变成了负向效应，并且达到负响应的最大值，到了第4个交易日又变为极为微弱的正向效应，到第5个交易日时正向效应逐渐减弱直至影响消失。说明收益率对自身所受到的冲击在初期反应非常敏感，但在5个交易日后影响几乎完全消失，持续时间较短。

图8 收益率对成交量变动幅度的脉冲响应图`

如图8当给成交量变动幅度一个正向冲击后，在初期，收益率表现出较强的正向效应，随后正向效应开始迅速减弱，第2个交易日接近0，第3个交易日时又出现微弱的正向效应，第4个交易日正向效应完全消失并变为负向效应，到第6个交易日时负向效应达到了最低值，第7个交易日又变成了正向效应，第9个交易日后响应完全消失。

图9 成交量变动幅度对收益率的脉冲响应图

如图 9，给收益率一个正向冲击，成交量变动幅度在初期表现出了很强的正向并在第2个交易日达到了最大值，紧接着正向效应迅速消失，并第3个交易日达到了最大负响应，随后负向响应迅速减弱，第5个交易日变为微弱的正向效应，第6个交易日时，正向效应变为负向响应，到第8个交易日变成正向效应，第9个交易日后影响完全消失。

图10 成交量变动幅度对自身的脉冲响应图

如图 10，当给成交量变动幅度一个正向冲击后，在初期，成交量变动幅度表现出了极其强烈的正向响应并且达到了最大值，但在第2个交易日强烈的正响应迅速消失，并且达到了最大负向响应，在第7个交易日时表现出微弱的正响应，紧接着正向响应减弱，到第8个交易日是正向响应完全消失并趋于稳定。

（六）方差分解分析

为了研究在本论文所建立的VAR（5）模型中成交量变动幅度和收益率的贡献大小，并对这两个变量之间相互影响的重要程度做出评价，本文使用了方差分解的方法。通过方差分解对所建的VAR（5）的动态特点，可以了解随机信息的相对重要性。

表7 对收益率的方差分解

从表 7中可以看出，收益率受到成交量变动幅度的影响，但是受到成交量变动幅度的影响极小，一直稳定在3.40%到3.62%之间，说明在研究收益率的时候，要同时关注收益率和成交量变动幅度这两个变量，不能只盯着收益率本身，但是要将更多的关注点放在收益率上，因为收益率主要还是受到来自自身冲击的贡献。

表8 对成交量变动幅度的方差分解

从表 8中可以看出，成交量变动幅度一直都受到收益率的贡献率的影响，并且一直稳定在6.1%左右，其间只有极为微小的波动。但成交量变动幅度大部分还是受到自身贡献率的影响，一直都有保持在93.9%左右。说明在研究成交量变动幅度的时候，也要同时关注收益率和成交量变动幅度这两个变量，而不能够仅仅依靠成交量变动幅度来判断其自身的变动，但是要将更多的关注点放在成交量变动幅度上，因为成交量变动幅度本身对成交量变动幅度的贡献程度非常大。

五、结论与投资建议

本文以成交量变动幅度和收益率为指标，对我国创立至今近12周年的创业板指数的量价关系进行研究得出了以下四点结论：

第一，创业板指数的收益率与成交量变动幅度之间具有单向的格兰杰因果关系（见表 6），成交量变动幅度的滞后期对收益率的当期没有影响，而收益率的滞后期可以影响成交量变动幅度当期值，违背了“量在价先”的规律。

第二，通过对脉冲响应函数分析（见图 7-10）可得，给收益率或成交量变动幅度一个正向冲击时，其对应的变量调整时间持续了5-9个交易日。

第三，方差分解结果（见表 7和表 8）说明成交量变动幅度对于收益率的贡献程度相对较小，只占3.6%左右，而收益率受到自身的影响高达96.4%左右，因此，收益率主要还是受到自身的贡献程度比较大。收益率对于成交量变动幅度的贡献程度相对较大，占了6.1%左右，影响比较稳定，但主要还是和收益率一样，受到自身的贡献程度比较大，高达百分之九十多。

第四，根据脉冲响应，我国的创业板指数从长期来看，并不具有持续的量价关系，但在短期内（10天内）具有一定的量价关系，这就表明了技术分析在短期是可以作为主要的分析手段使用的。

由上文的结论可以提出以下建议：对于短期投资来说，可以通过对收益率和成交量变动幅度之间的相互变动来预测股市的量价变化，这在很大概率上能够帮助投资者获利。从长期看，技术分析不应该成为创业板指数交易唯一的分析手段，而应该在技术分析的基础上，结合分析与创业板指数有关的公司的业绩，来判断购买创业板指数的时机，这有利于对投资者的长期收益进行预测。

参考文献：

[1]Chen S S. Revisiting the empirical linkages between stock returns and trading volume[J]. Journal of Banking & Finance, 2012,36(6):1781-1788.

[2]Clark P K. A Subordinated Stochastic Process Model With Finite Variance for Security Prices [J].Econometrica,1973,41(1):135-155.

[3]Crouch R L. The volume of transactions and price changes on the New York stock exchange [J].Financial Analysis Journal,1970,26(4):104-109.

[4]Dickey, D. and W. Fuller. Distribution of the Estimators for Autoregressive Time Series with a Unit Root[J].Journal of the American Statistical Association,1979(74),427-431.

[5]Karpoff, Jonathan M. The relation between price changes trading volume: A survey[J].Journal of Finance and Quantitative analysis, 1987,22(1): 109-126.

[6]Lutkepohl, H. New Introduction to Multiple Time Series Analysis[J]. Econometric Theory, 2005, 22(5):961-967.

[7]Osborne M F M. Brownian Motion in the Stock Market [J]. Operations Research. 1959,7(2):145-173.

[8]Sims, C. Macroeconomics and Reality[J].Econometrica,1980(48),1-48.

[9]邓怡,周紫焱.基于VAR模型的上海A股市场价量关系研究[J].时代金融,2015(23):276-278.

[10]南梦佳,王璐熠.股市量价关系研究[J].现代商贸工业,2016,37(18):97-98.

[11]史晓雁.中国股票市场快速放大的成交量与收益率关系的研究[D].北方工业大学,2019.

[12]熊连庆,刘煜辉.成交量能解释收益率的GARCH效应吗:中国市场的实证[J].数量经济技术经济研究,2004(3):134-139.

[13]张维,闫冀楠.关于上海股市量价因果关系的实证探测[J].系统工程理论与实践,1998(6):112-115.

[14]郑方镳,吴超鹏,吴世农.股票成交量与收益率序列相关性研究——来自中国股市的实证证据[J].金融研究,2007(3):140-150.